Using carabiners as pulleys

Tuomas Pöysti 2020

Once again, this is not a very practical article. Not a single photo. And I’m not going to give much direct answers or advice, but hopefully this will help someone coming into their own conclusions.

Using pulley system analysis, we can systematically study some properties of different pulley systems. For example, we may assume all pulleys are identical in efficiency and plot curves of the pulley system efficiencies as pulley efficiency varies.

Sample pulley systems

Here are couple of pulley systems, part of which were introduced in the linked article.

5:1 “crevasse” and a 7:1 variation, “double mariner” as Petzl calls it

Common 9:1 “Z on Z” and a 11:1 variation of it. Notice analogy with the previous pair.

The last one can be seen as a category, extra V’s may be added without limits – in theory at least.

A few words about analysis

The table below shows numbers of each degree terms in each pulley system’s calculated MA expression. See this article for clarification.

Because all pulleys are assumed identical, it is feasible just to count each degree terms. For example the 5:1 “crevasse” has MA expression:

1 + P2 + P3 + P1P2 + P2P3

we can write P1=P2=P3 = P, thus the expression becomes

1 + 2P + 2P^2

And this is exactly what the table says. This pulley system has the zeroth term “1”, two first degree terms and two second degree terms in it’s MA expression.

The sum of each row is the ideal MA of the corresponding pulley system. In a non-ideal situation, only the zeroth degree term “1” is not affected by the pulley inefficiency. The higher the degree, the bigger the infuence.

Curves

But now, some curves! Let’s start with simple pulley systems.

Calculated MA’s of some simple pulley systems when pulley efficiency varies between 0 and 1

Now that we are interested in how carabiners or such high-friction “pulleys” manage, let’s focus on the middle area of the plot. At 0.5, all curves neatly avoid hitting even MA 2:1. Especially notice the minuscule difference between 4:1 and 5:1.

Here’s the 5:1 compared to crevasse 5:1:

Both are ideally 5:1 and 1:1 in the worst case, but they connect the dots quite differently! The crevasse is some 25% better at 0.5.

Ideally, the curve should be a straight line. The simple 2:1 does just that, and it is not a surprise considering it’s expression 1 + P – a linear, first degree polynomial. It is the higher degree terms that bend the curve, and the higher degree, the more the curve will sag.

For example the two 5:1’s have same amount of terms, of course, but in the crevasse they come as lower degree versions. When the crevasse is converted to “double mariner” 7:1, the added two terms are of degree 2 and 3. The added MA at 0.5 pulley efficiency is

P^2 + P^3 = 0.25 + 0.125= 0.375

instead of the ideal 2. This is a great example of how higher degree terms can be summoned: the conversion adds a rope grab on the “wrong side” of P1.

The next plot is not very readable in detail, but the big picture is clear:

Practically all compared pulley systems do worse than 4:1 with 50% pulleys.

The highest MA at 0.5 is 5:1, delivered by 16:1 “V on V on V on V”. The “V biggyback” family is special in that they have all possible terms in their expressions. That is, they have the highest possible ideal MA at each number of pulleys.

But beyond 4:1 “V on V”, they are not very practical. The collapse ratio of the topmost pulley in the 16:1 is eight – this means that the pulley system has to be reset eight times for every hauled length of the whole system. In theory. In real life the rope stretch will increase this number even more, perhaps close to infinity if the pulley system is not very long.

Is effective 4:1 possible?

Let’s see how the more practical (?) pulley systems do:

Maybe, if a pulley-rope combination acted as a 60% effective pulley, it could be possible using an ideally 9:1 or 11:1 pulley system.

Here’s an interesting thing. One surely shouldn’t expect anything over 50% efficiency for a carabiner as a pulley, if there is rope involved. But some pulley systems allows for different line materials used among rope. As an example, the 5:1 crevasse and “double mariner” include an internal pulley, shown in blue in the schematics.

It can be shown that carabiners may work as pulleys as efficient as 65% if used with proper materials. The blue line could consist of tape or cord, for example. Read more about some of my test results in the other articles.

Let’s study “A”:

Pulleys P3 and P4 work with the blue line. The MA expression is

1 + P2 + P4 + P1P2 + P2P4 + P3P4 + P2P3P4

Let P1=P2=0.5 and P3=P4=0.65; the expression becomes

1 + 0.5 + 0.65 + 0.5*0.5 + 0.5*0.65 + 0.65*0.65 + 0.5*0.65*0.65 = 3.36

There’s a 15% enhancement to the 2.88:1 we get by replacing all 0.65’s with 0.5. So, at least in theory it may be worth noticing that in addition of certain pulleys having more effect on the pulley systems effective MA, a single pulley may also have different efficiencies at different locations. This is true for actual pulleys, too.

The fool’s tackle

One last thing. There is an interesting 4:1 pulley application, apparently popular among alpine guides. It is based on what’s sometimes called the fools tackle. Ironically, the one who named it seems to be the actual fool!

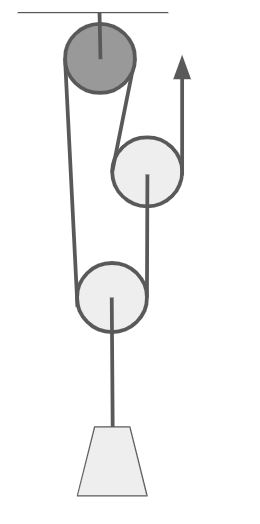
Namely, if the darker top pulley is inefficient enough, like a carabiner, only the two other pulleys will roll and the end result is like a normal V on V. With the exception that this version is very easy to reset. Google “mezzo poldo” and try it yourself!